目次
はじめに
みなさんこんばんは。「さんすうがく」の赤い小人です。
本日も「立体図形」の問題についてていねいに解説していきます！！
はい！よろしくお願いします！！
まずはじめに注意点です。今回の問題はかなりむずかしいです。
もし自信のない受験生がいたら、まずはこちらの問題から挑戦してみてください！！
自信のない受験生はこの問題からやってみよう！
図形を一回転させた時の体積比/側面積比/表面積比を求めるには？
今日の問題は今までの中でかなりむずかしいレベルになっていますので、さっそくヒントから説明していきます。
がんばっていきますよ！！
平面図形を回転させて立体図形にしよう
四角形が2つ重なった図形を回転させてみよう
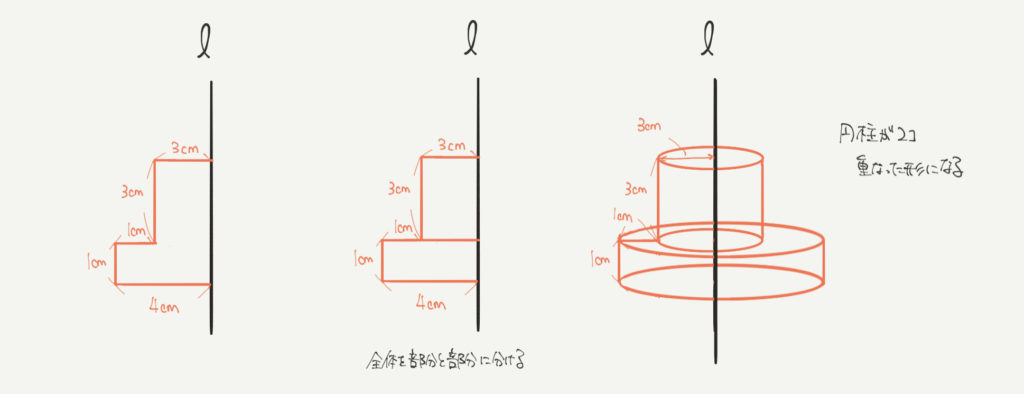
まずは四角形が2個重なった図形を回転させていきます。
このとき大切になってくる考えが「全体は部分と部分でできている」考え方です。
この図形は四角形が2個合わさってできているので、それぞれを回転させて考えてみましょう。
すると、右の図のような円柱が2つ合わさった図形が出来上がります！
三角形を回転させてみよう
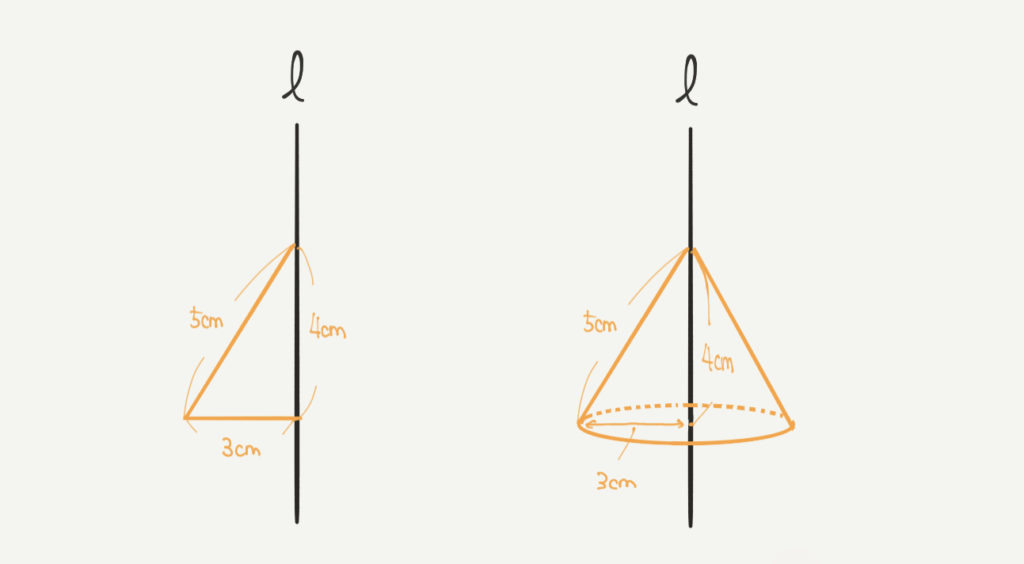
三角形を回転させるときはどうでしょうか？
これはそのままくるっと回転させてあげるとわかりやすいと思います。
底面の部分は半径3cmの円になり。上は回転してもほとんど動かないので円すいの形になりますね！
長方形を回転させてみよう
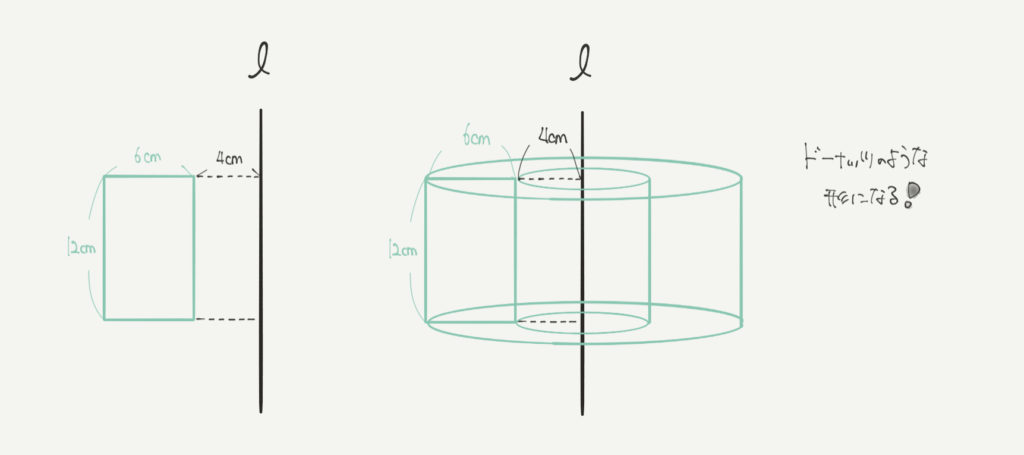
最後に軸から少しはなれたところにある長方形を回転させていきます。
ここでも「全体は部分と部分でできている」考え方を使いましょう。
この図形を回転させてできる形は、半径10cmの大きな円柱から、半径4cmの小さな円柱を引いた形になります。
ドーナッツみたいだね！
なので出来上がる図形は穴がぽっかり空いたような立体図形になります！
今回の問題では上の図形たちが出てきます。ぜひ参考に解いてみてください！
問題に挑戦！
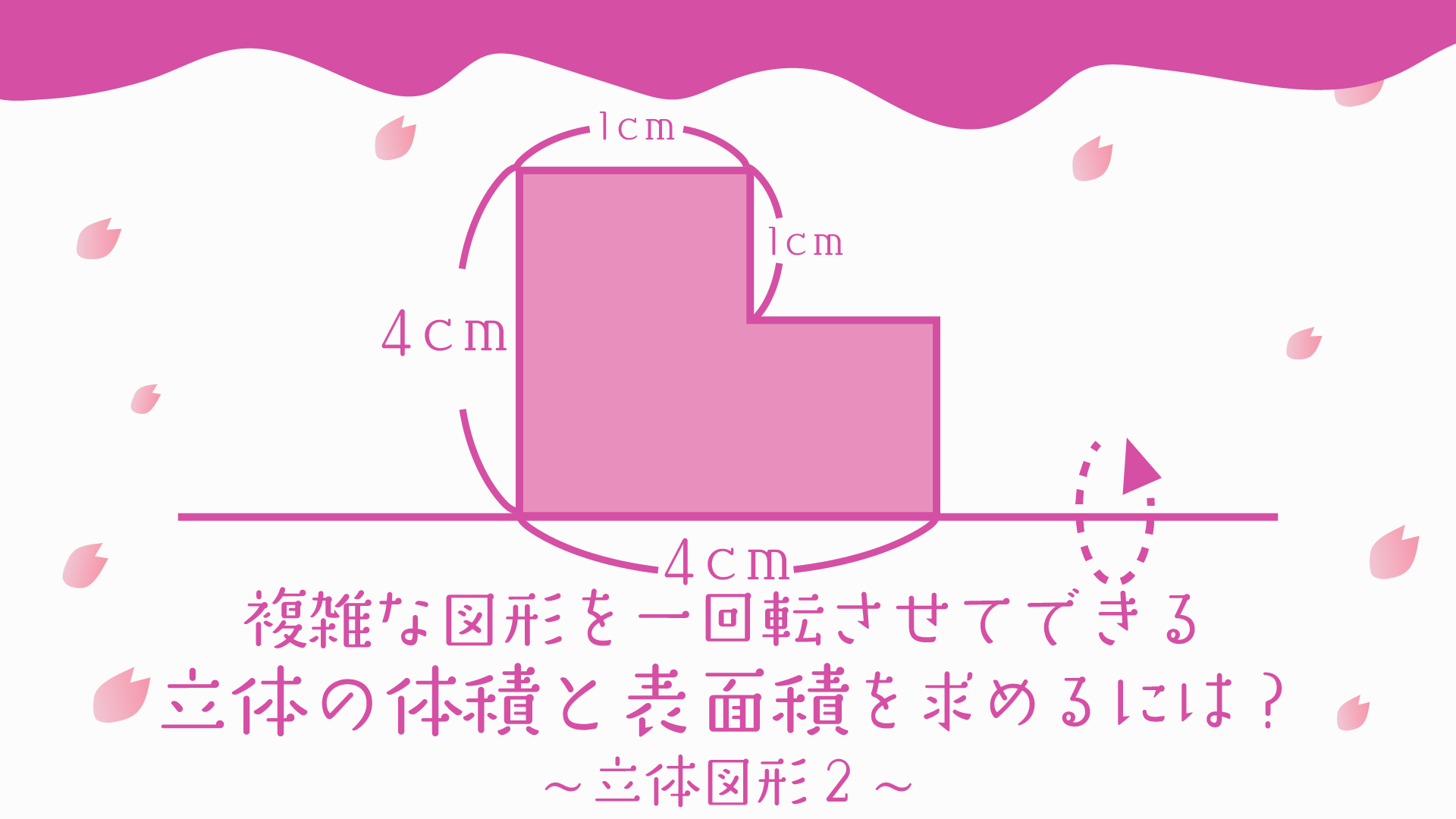
次の①〜③の図形を、直線ℓを軸として一回転させてできる立体について、体積と表面積をそれぞれ求めなさい。ただし、円周率は3.14とします。
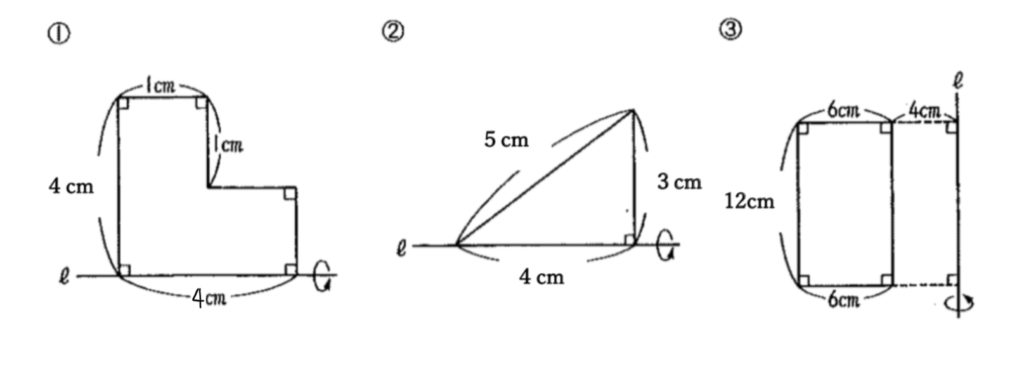
解答は次のページから！
- 1
- 2
